This is a basic task for all imagers: deciding on how many exposures to take or what exposure length to use.

Many factors influence the decision; two basic factors are the signal to be sensed and the read noise of the camera. These are basic and unavoidable first order parameters and by restricting our examination to these alone, insight can be gained into the exposure optimization task.

The basic signal to noise equation for a flat is what we will be examining. It can be shown that the S/N of a low contrast image is equal to the S/N of a flat field image when the average signal levels are the same and more specifically:

S/N(image) = M*S/N(flat field) where M is the modulation factor of the image.

This teaches that optimizing the S/N of a flat field image produces the highest S/N for an image.

Since flat field images are convenient to take and to analyze they provide an important tool for image S/N optimization.

For this analysis we are ignoring the noise associated with dark signal formation. This is easily justified by noting that cooling can be used to set the dark current at a level that creates insignificant noise during the period of the exposure. Insignificant noise means it is more than a factor of 10 less than the read noise of the camera. So we will ignore dark noise and dark fixed pattern noise.

Fixed pattern noise is ignored because it can be removed by flat-fielding. While it may seem silly to apply a flat to a flat, from a noise analysis perspective it makes perfect sense. So we will ignore fixed pattern noise.

The remaining significant noise sources are the shot noise of the signal itself ( =sqrt(signal)) and the read noise of the camera.

The S/N equation works out to be = Signal / Sqrt(Signal + rd_noise^2). This is what will be analyzed.

For an exposure comprised of K subexposures of Signal/K, the noise becomes

Signal / Sqrt(Signal + K*rd_noise^2)

If the rd_noise is non-zero then 10 exposures of n seconds will give a lower s/n ratio than a single exposure of 10*n seconds looking solely at these parameters. How much lower depends on the relative magnitude of the signal shot noise and the read noise.

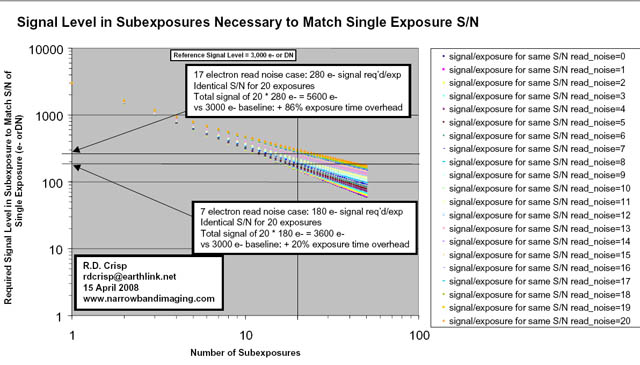
With non-zero read noise the S/N will be degraded when multiple subexposures are summed compared to a single exposure of the same total time. For the multiple subexposure case, it is possible to match the S/N of the single exposure case by increasing the subexposure time or by picking a subexposure time and adjusting the number of exposures.

The purpose of this analysis is to derive a relationship for K subexposures of time Tk that provides the same S/N as a single exposure of a lesser time T. A second purpose of this analysis is to derive an expression for N subexposures of chosen level K such that the resulting S/N ratio is the same as a single exposure. So one way picks the number of exposures and calculates the exposure level necessary, while the other picks the exposure level and calculates the number of exposures to reach the same S/N as the single exposure.